こんな逆張りトレードしたことありませんか？
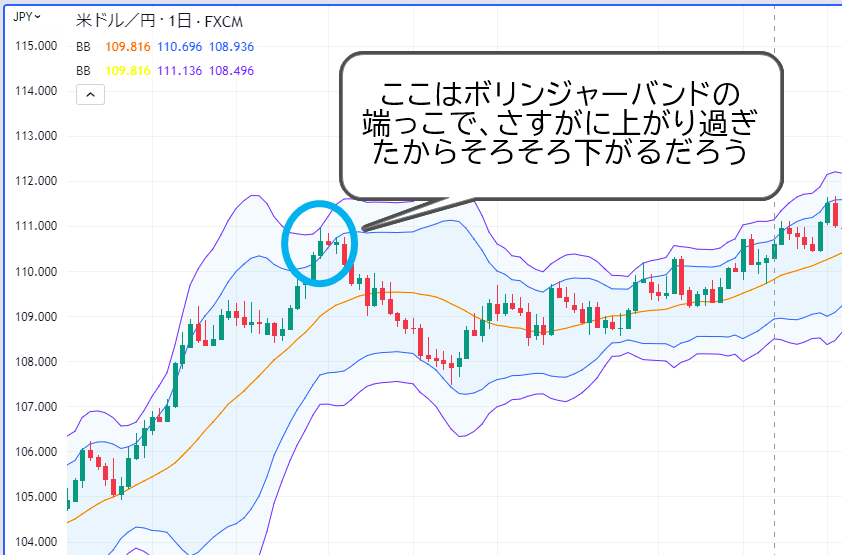
上記はボリンジャーバンドを表示したドル円のチャートです。
ボリンジャーバンドの外側にタッチで、「ここはどう見ても行き過ぎ！逆張りショートのエントリーチャンス！」なんてことは誰でも一度は考えたことがある場所かと思います。
しかしこの「行き過ぎ」という考えは、戻るべき基準価格があっての発想です。
取り扱っているデータが正規分布（ランダムに動いている）している時のみに有効であり、正規分布していないデータは、価格が上か下かに偏っているので通用しません。
正規分布しているデータとは？
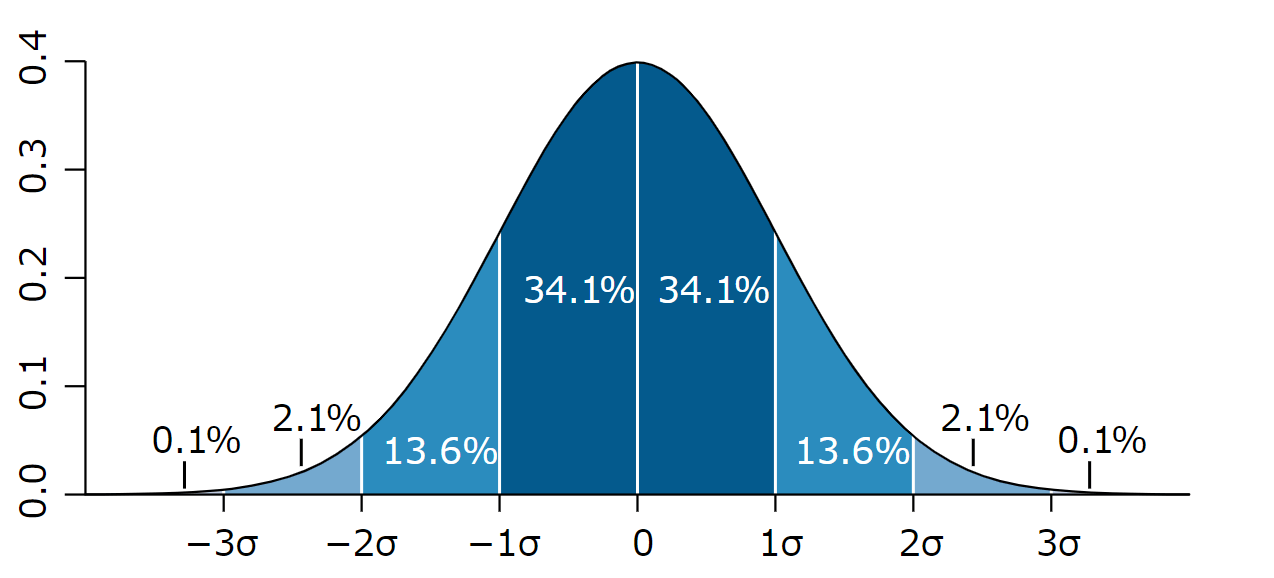
正規分布とは、統計学でよく使われる「釣鐘型（つりがねがた）」のグラフを描くデータの散らばり具合です。
ベルのような形状から「ベルカーブ」とも呼ばれ、統計の世界では最も重要と言っていいほどの分布です。
データの多くが中心に集まっていて、両端に行くほどデータが少なくなる形状をしており、例えばクラスのテストの点数が正規分布に従っているとすると、平均点の周辺（中央付近）に多くの生徒がいて、高得点や低得点の生徒は両端に分布されて少なくなります。
そして正規分布しているデータというのは変なバイアスがかかっておらず、正規分布の範囲の中で完全にランダムに動いていることを表します。
正規分布しているデータの呼び方ですが、中央が0、と中央に近い方から両端に向かって±1σ（シグマ）、±2σ、±3σというように広がっていきます。
正規分布を実例で見てみましょう
さて、一旦難しい話は置きまして、正規分布がランダムなデータだと直感的にわかる動画で見てみましょう。
下記の動画はガルトンボードというおもちゃの動画です。
ガルトンボードは上部の中央から大量の小さな球を流すと12段に別れた杭に当たりながらランダムに下の仕切りに散らばっていきます。
球は杭に当たるたびに1/2の確率で左右に別れていき、最終的には下の溝に溜まっていきます。
これが何を意味しているかと言うと、例えば杭に当たるたびに右→右→右→右→右→右→右→右→右→右→右→右とすべて右へ転がった球は一番右側にはいり、逆に左→左→左→左→左→左→左→左→左→左→左→左と転がった球は一番左にはいります。
杭に球があたって転がる方向は1/2の確率で「左と右」に分かれますので、全て同じ方向に流れなければたどり着けない端っこは、かなりレアな現象ということになります。
そのため、中央が高くて両端が低くなる正規分布に収まるわけですね。
この正規分布の形は非常に重要で、もしデータが正規分布している株価ならば、一番端の3σまで株価が飛んでも、それは非常にレアケースということが言え、いずれ中央の平均値に戻ってくることが期待できます。
正規分布していないデータとは？
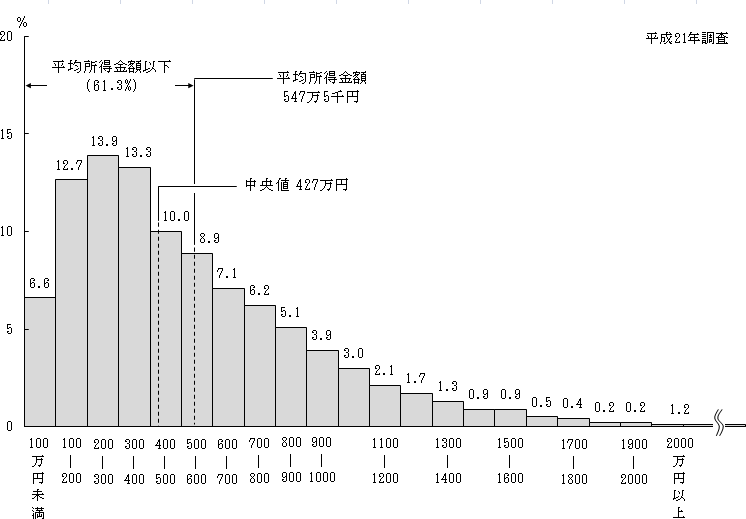
次に正規分布していないデータ、つまりランダムではないデータもご紹介しておきましょう。
上記の画像は正規分布していない例としてよく出される、「世帯別の収入」です。100万円ごとに区切っていますが左側に偏っていますね。上限の位置もよくわかりません。
このデータを見て、「国民の平均所得は549万円6千円！」なんて言われても、実生活を考えるといまいちピンと来ないですよね。
この偏っているタイプのデータですが、株や為替のデータがそのまま当てはまります。経済が成長する限り株価には上昇の力が加わりますし、為替ならば2国間の関係が完全に均等でない限りは上下どちらかに力が加わります。
そんなデータにボリンジャーバンドを表示して「価格が行き過ぎだからいずれ下がるはず！」といってエントリーしても、データが偏っていますので当然価格が戻ってこないことが頻繁に起こります。
正規分布している株価データの見つけ方
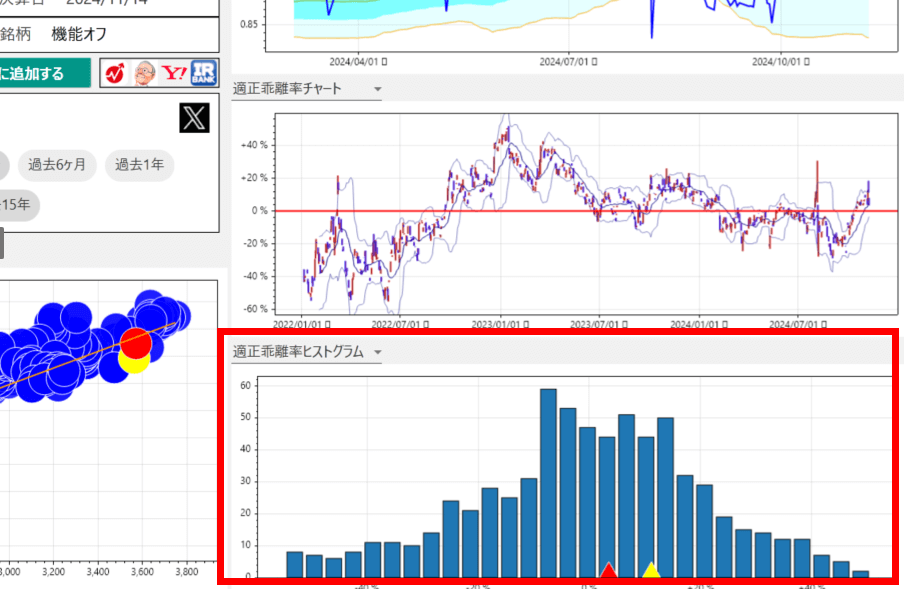
株価が正規分布しているかどうかですが、残念ながら企業単体の銘柄で正規分布しているものは存在しません。
これは会社が「成長し続けることを目的」としているためで、ほぼ全ての株価に一方向の値上がりバイアスがかかっているからです。
そこで1つの方法として、似たような動きをする2銘柄のサヤ（価格差）だけに絞って分析する方法があります。
例えば『イオン㈱』と『イオン北海道株式会社』ですが、イオン北海道はイオンの子会社で、2つは同じ業態なので株価は似たような動きをします。景気が上向けば両社とも株価は上がり、コロナでは両社とも大きく株価が下がりました。
もし社内で大ヒットした商品があれば両社で共有されますし、イオンの組織改革でうまく機能した事例や失敗した事例は、イオン北海道でも共有されます。
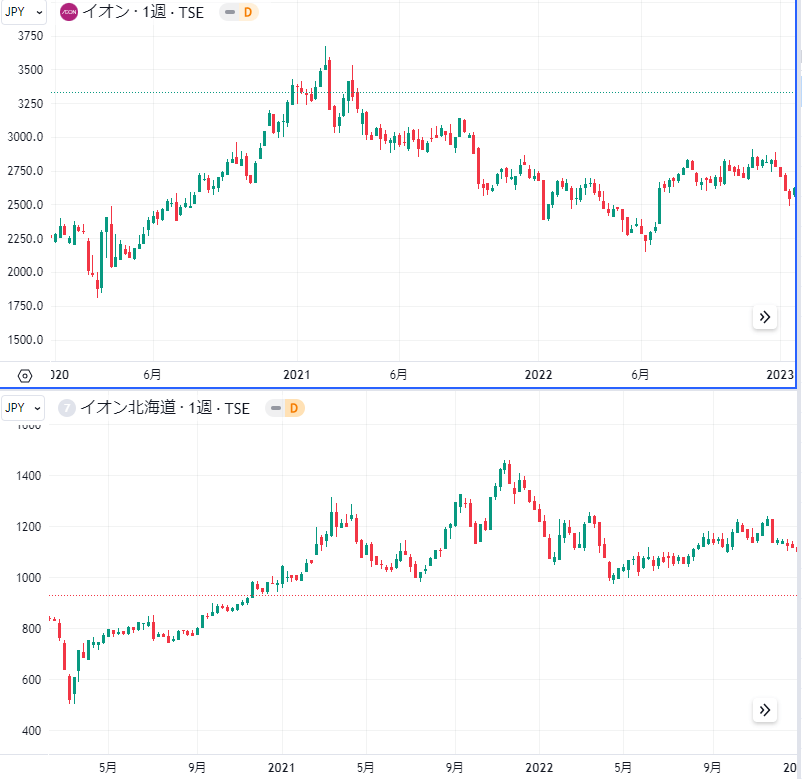イオン㈱とイオン北海道株式会社の株価比較、似た動きをしていますね。
ということは、両社の株価の動きは、どちらかが一方的に上がり、どちらかが一方的に下がるということは起こりにくく、両者の株価は一定の価格差（サヤ）を保ったまま動きます。
そしてこの『一定の価格差』というのが、実は先程お話した『正規分布の中央値』として利用することができます。
つまりどちらかの株価が行き過ぎても、時間が経てば『一定の価格差』に戻ってくるというわけなので、この価格差が広がった時に価格が高い銘柄を売り、安い銘柄を買って両建てし、価格差が戻った時に両建てを決済すれば利益が得られるということです。
当サイトで公開しているBLSシステムを使うと、2銘柄のサヤが正規分布しているかどうかに加えて、サヤが開いているのかどうかも一目でわかります。
正規分布している日本とアメリカの経済
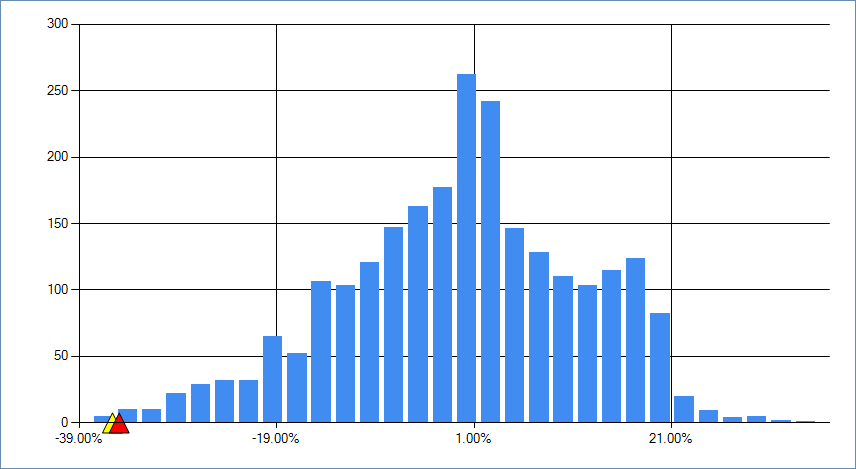こちらは日経225と米国S&P500のサヤの散らばり
上記は日経225インデックスと米国S&P500インデックスの価格差の分布です。ちょっと右肩が出っ張っていますが、ほぼ正規分布の形に近くなっていますね。
なぜこのように正規分布の形になるのかには理由がありまして、それは日本と米国との経済は密接な関係にあるからです。
アメリカには多くの日本企業が進出していますし、日本にも多くのアメリカ企業が進出しています。クレジットカードやスマートフォンなど、日本人が何気なく使っているものの多くがアメリカの利益に直結しているので、日本の不景気はアメリカにも影響がでます。
また、アメリカと日本の貿易関係に限って言うと、円高になれば日本の輸出企業は落ち込みアメリカの輸出企業が潤い、逆に円安になれば日本企業が潤いアメリカの企業は落ち込みます。
いろいろな要因がありますが、このように経済を共存していると、ビルトインスタビライザー（経済の自動調整機能）が働きますので、どちらかだけが行き過ぎるといったことが起こりにくく、サヤの散らばりは正規分布を描きやすくなるのです。
BLSシステム有料プラン2週間おためしチケット
BLSシステムの無料版では日経225銘柄の正規分布やサヤの分析が可能ですが、有料版では東証プライムやスタンダード、東証2000などの分析まで可能になります。
BLSシステムを初めてご利用の方は、自動で2週間有料版がご利用できますので、ぜひお試しください。
正規分布していない価格データでトレードしてはいけない まとめ
